1. Valid Parentheses
1.1 Using Stacks
🎯 Understanding the Test Cases:
Test Case 1:
Input: s = "[()]"
Explanation: The string "([])" is valid because each open bracket has a matching closing bracket, and they close in the correct order. Since all brackets are properly paired, the string evaluates to True.
Test Case 2:
Explanation: The string "(]" is invalid because the open bracket ( is not closed by the correct type of bracket. The closing bracket ] doesn’t match the opening (, so the string evaluates to False.
🔍 Problem Understanding:
We only have three types of brackets: [], (), {}. And we need to close the last opened bracket first. What do you do when you need to close the last opened bracket first? You need a system where the last thing you add is the first thing you take out, right? This is the Last In, First Out (LIFO) system. So, what data structure works best for LIFO? A stack! A stack can help us keep track of the brackets. Whenever we find an opening bracket, we push it onto the stack. When we encounter a closing bracket, we pop the stack to see if it matches the last opened bracket.
Let’s say you’ve read the first two characters of a string and added them to the stack. Your stack might look like this:
stack = ['(', '{'].
Now, what if the next character is }? How do you know if this closing bracket matches the last opened one? To figure this out, we can use a simple mapping: each closing bracket corresponds to its opening bracket, like this: closing bracket : Corresponding opening bracket. This way, we can check if every closing bracket matches the correct opening one.
⚠️ Edge Cases:
What happens if you have opening brackets left in the stack, but the string ends? Or what if there are closing brackets, but the stack is empty? How would you handle these situations?
Time Complexity: \(O(n)\)
Space Complexity: \(O(n)\)
Need help with implementation?
class Solution:
def isValid(self, s: str) -> bool:
# Keep the mapping as 'closing bracket' : 'Correspoding opening bracket'
mapping = {
')' : '(',
']' : '[',
'}' : '{'
}
stack = [ ]
# O(n)
for char in s:
if char not in mapping: # This means that the bracket is an open bracket
stack.append(char) # Simply add the open bracket to the stack
else:
# Corner case- stack has no elements but the string has closing bracket
if len(stack) == 0:
return False
# Check if opening bracket in the stack matches with the closing bracket in the string
if mapping[char] != stack.pop():
return False
# if stack is empty after checking every char of string
# that means that we found the closing bracket for every opening bracket. Thus, return True
# And vice versa. Return False
return not stack # Returns True if stack is empty, False otherwise
2. Longest Consecutive Sequence
🎯 Understanding the Test Cases:
Test Case 1:
nums=[100, 4, 200, 1, 3, 2]
Explanation:
The longest consecutive sequence in the array is [1, 2, 3, 4], which has a length of 4. Note that it is okay if the numbers do not appear contiguously or as a subsequence in the array. For example, in this the number 4 occurs before the the other numbers in the sequence. All that we are asked is to return the length of the longest sequence whose elements are consecutive integers.
2.1 Brute Force
Can you think of a brute force way to solve this problem? You would look at each number and then search the entire array to see if the next number exists. You would do this for each element in the array, and keep track of the longest one.
But what’s the problem with this approach? It takes a lot of time—specifically, the time complexity is \(O(n^2)\). But we’re asked to find a solution that’s faster, with a time complexity of \(O(n)\).
2.2 Improved Approach Using Sets
When using brute force, we had to search the entire array to check if the next number existed. Do you think there’s a way to speed up this check? What if we had a data structure that allows us to check if a number exists in constant time?
Think of a data structure that has constant-time lookups.
We can use a set here!
So, how can we solve this using sets?
- For each number, while the next consecutive number exists, we keep counting.
- But wait! If we use this method directly, some numbers might get checked more than once, which still gives us \(O(n^2)\) time. How can we improve this?
Which numbers can start a consecutive sequence?
- Only those numbers
nwheren-1is not in the set. Only these numbers can be the starting points of the longest consecutive sequence. Do you see why? - By finding these starting points, we can run our loop efficiently on only these elements.
Time Complexity: \(O(n)\) Space Complexity: \(O(n)\)
Need help with implementation?
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
# Convert nums to a set
num_set = set(nums)
starting_points = set()
# Only those elements can be starting points where n - 1 is not in num_set
# O(n)
for num in nums:
if num - 1 not in num_set:
starting_points.add(num)
max_length = 0
# Overall O(n), because the inner while loop is just going to run once for other elements
for current_num in starting_points:
current_length = 1
while current_num + 1 in num_set:
current_num += 1
current_length += 1
max_length = max(max_length, current_length)
return max_length
Before you jump into these problems, here are some tips on solving linked list problems:
- Debugging linked lists can be a nightmare! So, it’s always better to get the code right the first time.
- When solving Linked List problems, it ALWAYS helps to draw the diagrams.
- Whenever you see a Linked List problem, the first thing that you should do is: handle the base / edge cases like an empty linked list or a list with just one node. It’ll save you a lot of time and stress, especially during the OPPE!
3. Rotate List
3.1 Rotation Logic:
- If \(k \gt n\), then the number of effective rotations is: \(k = k \% n\).
- Think about this as a three step problem:
- First, traverse \(k\) nodes. This
n - kth node becomes thenewheadof the rotated list. - Next, connect the original list’s tail to its
headto create a cycle in the linked list. - Finally, walk from the
newheadfornnodes to find thenewtail, which will become the tail of the rotated list by marking its next pointer as None.
- First, traverse \(k\) nodes. This
Note: Readers are encouraged to look for cleaner and more efficient solution on the platform and take this approach as a starting point.
Need help with implementation?
class Solution:
# Gets the length of node: 'n'
def get_length(self, head):
current = head
count = 0
while current:
current = current.next
count += 1
return count
def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
n = self.get_length(head)
# Corner case
if n <= 1:
return head
k = k % n # Number of effective rotations
# In the original list, you need to walk these many steps to get to new head
walk_these_many_steps = n - k
if k == 0 or walk_these_many_steps == 0:
return head
# Get the new head of the list that you will get after you rotate
current = head
count = 0
newhead = None
while current:
if count == walk_these_many_steps:
newhead = current
break
current = current.next
count += 1
# Get to the end of the list so that you can link tail with the head.
# But now your linked list is a cycle
current = head
count = 0
while current:
if not current.next:
current.next = head
break
current = current.next
# Now you need to make the new tail point to None to break the cycle
current = newhead
count = 0
while current and count < n:
current = current.next
count += 1
if count == n - 1:
current.next = None
return newhead
4. Swap Nodes in Pairs
4.1 Intuition
Let’s break this problem down step by step with the help of an image. Imagine we have a linked list, and we want to swap every two nodes. To make this easier, we’ll look at an illustration. We’re going to use some colors and a little helper node.
We make a dummy node at the front of the list. This dummy points to the head and we’ll call it
prevfor “previous”. It’ll help us easily swap the first two nodes.In each step, we’ll change certain links between nodes. These important links will be marked in pink.
To swap the nodes, we use pointers, shown in blue. These pointers help us know which nodes we’re swapping and how to connect them.
Next to the diagram of each step, we’ll show simple code steps for changing the links.
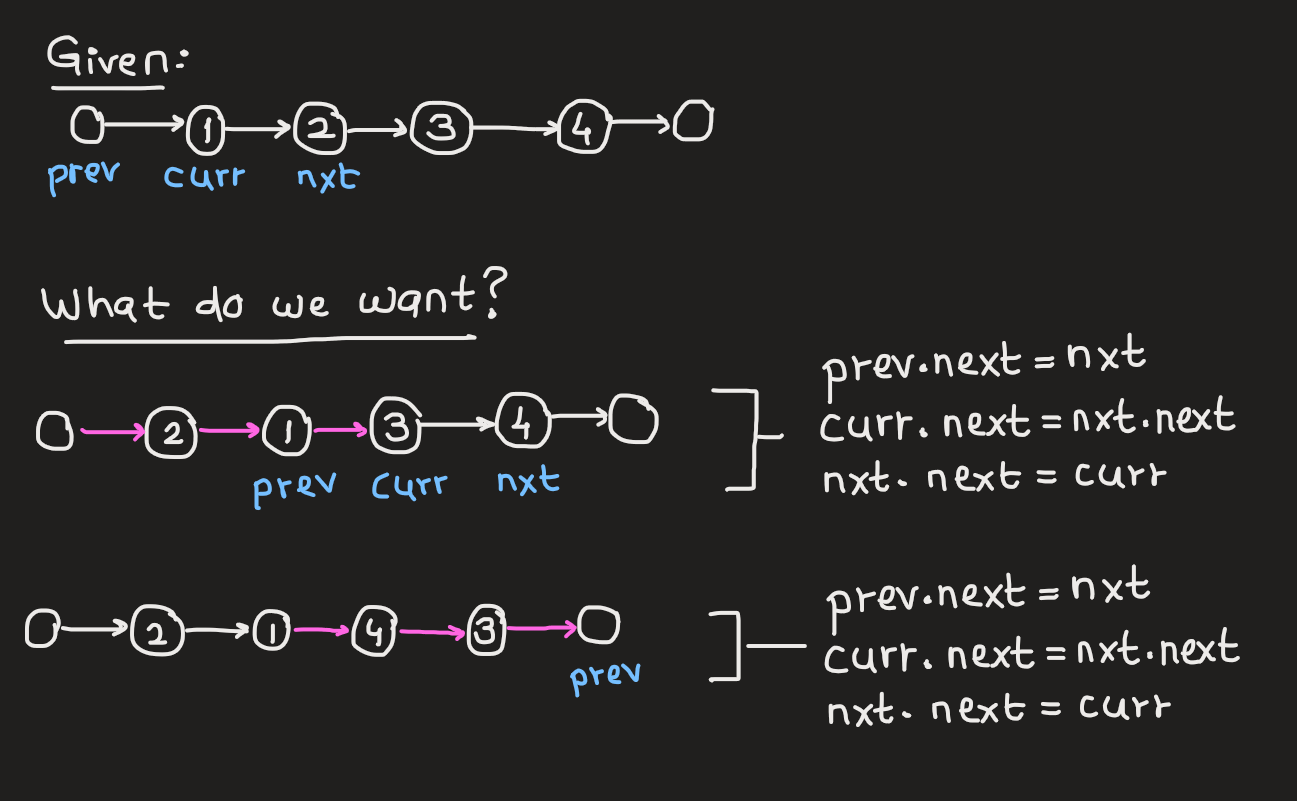
Now let’s code this!
Need help with implementation?
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
# Create a Dummy node that becomes "prev"
dummy = ListNode(0)
dummy.next = head
prev = dummy
# Since we are going to update using prev.next and prev.next.next
# they both should exist
while prev.next and prev.next.next:
# Find the "curr" and "nxt" nodes
curr = prev.next
nxt = prev.next.next
# Pink links for swap
prev.next = nxt
curr.next = nxt.next
nxt.next = curr
# Move the "prev" pointer to the next pair
prev = curr
# The new head of the list is next to the dummy node
return dummy.next
5. Reverse Nodes in K Groups
5.1 Using Recursion
Intuition:
You know how to reverse a linked list from the Graded Assignment question. Given a number k, can you reverse the first k nodes and return the head and tail after reversing? Now that we have reversed the first k nodes, can you repeat the same thing for the next k nodes? We have a way of reversing groups of k nodes. But here’s the important part: how do you connect these reversed groups?
🤔 Can you think of a recursive way?
- Remember that the last reversed
knodes will be the first to return when called recursively! - Let’s take an example list:
1 -> 2 -> 3 -> 4, andk = 2.- First, reverse
1 -> 2as2 -> 1, and return the head as2and tail as1. - Then, reverse
3 -> 4recursively as4 -> 3, and return the head as4and tail as3. - Now, you just need to connect the tail of the first reversed group (1) to the head of the second reversed group (4). Voilà! You’ve connected the reversed groups.
- First, reverse
Need help with implementation?
class Solution:
# Helper function: returns the number of nodes in the linked list
def get_length(self, head):
count = 0
current = head
while current:
current = current.next
count += 1
return count
def reverse(self, head, k, n):
# Edge Case: The group is empty
if not head:
return head, None
# Edge case: If k > n, then remaining nodes should remain as they are
if k > n:
return head, None
# Reverse the K nodes in groups starting from "head"
current = head
prev = None
next_node = None
count = 0
while current and count <= k:
# Counting because we want to mark the tail also
if count < k:
next_node = current.next
current.next = prev
prev = current
current = next_node
count += 1
curr_head = prev # The head of the reversed k nodes
curr_tail = head # tail of the reversed k nodes
# Recursively call reverse on the next k nodes. Observe that the number of nodes in remaining list is: n - k
next_head, next_tail = self.reverse(next_node, k, n - k)
# Connect the current group's tail with the head of the next group
curr_tail.next = next_head
return curr_head, curr_tail
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
n = self.get_length(head)
head, tail = self.reverse(head, k, n)
return head
6. Middle of The Linked List
6.1 Using Iteration
Let’s think about how we can find the middle element in a linked list, similar to how we do it in an array. We usually find the middle index by calculating mid = len(L) // 2 and then return L[mid]. This works because arrays let us access any element directly by its index.
But in a linked list, we don’t have direct access to an element by index. So, how could we find the middle element?
Here’s how:
- First, we need to compute
len(L). How can we do this? We could iterate through the entire list, counting each node as we go. - Once we know the length, we can compute the middle index just like we did with the array:
mid = len(L) // 2 - Finally, we would traverse the list again, stopping when we reach the middle node.
Time Complexity: \(O(n)\)
Need help with implementation?
class Solution:
def get_length(self, head):
"""
Helper function- iterates over the entire linked list and returns the length of the list
"""
counter = 0
while head:
counter += 1
head = head.next
return counter
def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
# Handle the base case
if not head:
return
# Compute the middle index
n = self.get_length(head)
mid = n // 2
# Iterate mid number of steps
idx = 0
while idx < mid:
head = head.next # note that we are updating the head. So after "mid" iterations, head = middle node
idx += 1
# Since head = mid after iterating, we return head
return head
7. Delete the Middle Node
7.1 Using Iteration
We’ve already discussed how to find the middle node in a linked list. So, if we know how to reach the middle node, can we figure out how to delete it? 🤔
To delete a node in a linked list, here’s what we need to do:
- Stop at the node before the one we want to delete.
- Redirect the pointer: Change the next pointer of the current node to skip the node we want to delete and point to the node after it. Essentially,
current.next = current.next.next.
⚠️ Edge Cases: What if the linked list has only one node? In this scenario, we need to handle cases where current.next.next doesn’t exist.
- Time Complexity: \(O(n)\)
Need help with implementation?
class Solution:
def get_length(self, head):
"""
Helper function- iterates over the entire linked list and returns the length of the list
"""
counter = 0
while head:
counter += 1
head = head.next
return counter
def deleteMiddle(self, head: Optional[ListNode]) -> Optional[ListNode]:
mid = self.get_length(head) // 2
current = head # Iterate using current because we want to return the head
idx = 0
# Stopping one node before the middle node
while idx < mid - 1:
current = current.next
idx += 1
# Change links of the node before to the next to next node by handling corner case
if current.next and current.next.next:
current.next = current.next.next
else:
current.next = None
return head
8. Delete nth Node From End
8.1 Using Iteration
We now know how to delete the middle node. Can you try to solve this problem using the ideas from that question?
Hint: Deleting the nth node from the end is the same as deleting (length - n)th node from the front.
9. Merge Two Sorted Lists
Remember Merge Sort algorithm? Can you see how this question is similar to the merge(A, B) operation from the merge sort algorithm? Only instead of merging arrays, we’re merging linked lists! 🔗
Need help with implementation?
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
# Dummy node to serve as a proxy for head of the list to return
dummy = ListNode()
current = dummy
# Iterate as long as neither list is exhausted
while list1 and list2:
if list1.val < list2.val:
current.next = list1
list1 = list1.next
else:
current.next = list2
list2 = list2.next
current = current.next
# Attach the remaining nodes of list1 or list2
if list1:
current.next = list1
elif list2:
current.next = list2
# The merged list is next to the dummy node
return dummy.next